Impact of population mixing between vaccinated and unvaccinated subpopulations on infectious disease dynamics: implications for SARS-CoV-2 transmission - CMAJ
Abstract
Background: The speed of vaccine development has been a singular achievement during the COVID-19 pandemic, although uptake has not been universal. Vaccine opponents often frame their opposition in terms of the rights of the unvaccinated. We sought to explore the impact of mixing of vaccinated and unvaccinated populations on risk of SARS-CoV-2 infection among vaccinated people.
Methods: We constructed a simple susceptible–infectious–recovered compartmental model of a respiratory infectious disease with 2 connected subpopulations: people who were vaccinated and those who were unvaccinated. We simulated a spectrum of patterns of mixing between vaccinated and unvaccinated groups that ranged from random mixing to complete like-with-like mixing (complete assortativity), in which people have contact exclusively with others with the same vaccination status. We evaluated the dynamics of an epidemic within each subgroup and in the population as a whole.
Results: We found that the risk of infection was markedly higher among unvaccinated people than among vaccinated people under all mixing assumptions. The contact-adjusted contribution of unvaccinated people to infection risk was disproportionate, with unvaccinated people contributing to infections among those who were vaccinated at a rate higher than would have been expected based on contact numbers alone. We found that as like-with-like mixing increased, attack rates among vaccinated people decreased from 15% to 10% (and increased from 62% to 79% among unvaccinated people), but the contact-adjusted contribution to risk among vaccinated people derived from contact with unvaccinated people increased.
Interpretation: Although risk associated with avoiding vaccination during a virulent pandemic accrues chiefly to people who are unvaccinated, their choices affect risk of viral infection among those who are vaccinated in a manner that is disproportionate to the portion of unvaccinated people in the population.
The remarkable speed of vaccine development, production and administration during the COVID-19 pandemic is a singular human achievement.1 While the ability to vaccinate to herd immunity has been held back by the increasing transmissibility of novel SARS-CoV-2 variants of concern (e.g., Delta and Omicron variants),2,3 and global distribution of vaccines is inequitable,4 the effectiveness of SARS-CoV-2 vaccines in reducing severity of disease and disrupting onward transmission even when breakthrough infections occur is likely to have saved many lives. The emergence of the immune-evasive Omicron variant may undermine some of these gains, although provision of booster vaccine doses may restore vaccination to a high level of potency, and vaccines developed specifically to enhance immunity to the Omicron variant may emerge in 2022.3,5–7
However, antivaccine sentiment, fuelled in part by organized disinformation efforts, has resulted in suboptimal uptake of readily available vaccines in many countries, with adverse health and economic consequences.8–10 Although the decision not to receive vaccination is often framed in terms of the rights of individuals to opt out,11,12 such arguments neglect the potential harms to the wider community that derive from poor vaccine uptake. Nonvaccination is expected to result in amplification of disease transmission in unvaccinated subpopulations, but the communicable nature of infectious diseases means that this also heightens risk for vaccinated populations, when vaccines confer imperfect immunity. Although assortative (like-with-like) mixing13 is characteristic of many communicable disease systems and may be expected to limit interaction between vaccinated and unvaccinated subpopulations to some degree, the normal functioning of society means that complete like-with-like mixing is not observed in reality. Furthermore, the airborne spread of SARS-CoV-214–20 means that close-range physical mixing of people from vaccinated and unvaccinated groups is not necessary for between-group disease transmission.
Historically, behaviours that create health risks for the community as well as individuals have been the subject of public health regulation. This is true of communicable infectious diseases but also applies to public health statutes that limit indoor cigarette smoking21 and legal restrictions on driving under the influence of alcohol and other intoxicants.22,23
Simple mathematical models can often provide important insights into the behaviour of complex communicable diseases systems.13,24,25 To better understand the implications of the interplay between vaccinated and unvaccinated populations under different assumptions about population mixing, we constructed a simple susceptible–infectious–recovered model to reproduce the dynamics of interactions between vaccinated and unvaccinated subpopulations in a predominantly vaccinated population. We sought to contrast contribution to epidemic size and risk estimates by subpopulation, and to understand the impact of mixing between vaccinated and unvaccinated groups on expected disease dynamics.
Methods
Model
We constructed a simple compartmental model of a respiratory viral disease.26 The model is described in Appendix 1 (available at www.cmaj.ca/lookup/doi/10.1503/cmaj.212105/tab-related-content). People are represented as residing in 3 possible "compartments:" susceptible to infection (S), infected and infectious (I), and recovered from infection with immunity (R). We divided the compartments to reflect 2 connected subpopulations: vaccinated and unvaccinated people. Susceptible people move into the infectious compartment after effective contacts (i.e., contacts of a nature and duration sufficient to permit transmission) with people who are infected. In the context of an airborne virus like SARS-CoV-2,14–20 effective contact may be conceptualized as "sharing air" with an infective case. After an infectious period, infectious people with SARS-CoV-2 recover with immunity. We also assumed that some fraction of the unvaccinated population had immunity at baseline owing to previous infection and that a fraction of the population was vaccinated. We treated immunity after vaccination as an all-or-none phenomenon, with a fraction of vaccinated people (as defined by vaccine effectiveness) entering the model in the immune state and the remainder being left in the susceptible state. For example, a vaccine that is 80% efficacious would result in 80% of vaccinated people becoming immune, with the remaining 20% being susceptible to infection. We did not model waning immunity.
Humans do not mix randomly and exhibit a tendency to interact preferentially with others like themselves,13,27 a phenomenon referred to as "assortativity." The relative frequency of interactions between people within different groups occurs on a spectrum that lies between high assortativity (i.e., like-with-like mixing) and random mixing. For instance, age-assortative mixing is frequently observed; children are more likely to interact with other children than would be expected if contacts occurred at random across all age groups. The use of matrices to govern such interactions are described in Appendix 1.
However, with respect to contacts between people from 2 different groups, relative frequency of contacts will depend both on the relative size of the 2 groups and the degree of like-with-like mixing. In our model, like-with-like mixing is determined by a constant (η), with random mixing occurring when η = 0, complete like-with-like mixing occurring when η = 1 and intermediate degrees of like-with-like mixing occurring at intermediate values. For our model, with 20% of the population unvaccinated, when random mixing is assumed (η = 0), 20% of the contacts a vaccinated person has would be expected to occur with unvaccinated people. When exclusively like-with-like mixing is assumed (η = 1), 0% of contacts a vaccinated person has would be with unvaccinated people. For intermediate levels of like-with-like mixing (η = 0.5), 10% of a vaccinated person's contacts would be with unvaccinated people.
We otherwise parameterized our base case model to represent a disease similar to SARS-CoV-2 infection with Delta variant, with a reproduction number of an infectious disease in the absence of immunity or control (R0) of 6,28 and we used higher values to capture the dynamics of the Omicron variant.29 Our lower-bound estimate for vaccine effectiveness (40%) reflected uncertainty about the emerging Omicron variant,3,7 whereas our upper bound (80%) reflected the higher effectiveness seen with the Delta variant.30 Base case parameters, plausible ranges and relevant references are presented in Table 1.
Model parameters
We used the model to explore the impact of varying rates of immunization and different levels of like-with-like mixing on the dynamics of disease in vaccinated and unvaccinated subpopulations. We evaluated the absolute contribution to overall case counts by these subpopulations, and within-group and overall infection risk. We calculated attack rates as the cumulative number of infections divided by the population size. We calculated a quantity (ψ), which we defined as the fraction of all infections among vaccinated people that derived from contact with unvaccinated people, divided by the fraction of all contacts that occurred with unvaccinated people. Effectively, this represents a normalized index of the degree to which risk in one group may be disproportionately driven by contact with another. For example, if 10% of contacts among vaccinated people are with unvaccinated people, but 50% of infections among vaccinated people derive from these contacts, ψ would have a value of 5. If infection were simply a function of frequency of contact between the groups and prevalence was the same across groups, ψ would have a value of 1. The value of ψ would increase above 1 either because of an increased fraction of infections derived from contact with unvaccinated people or a decrease in the amount of contact between the groups (i.e., an increase in like-with-like mixing).
A version of the model in Microsoft Excel is available at 10.6084/m9.figshare.15189576.
Ethics approval
Because this study involved the use of publicly available aggregate data, approval by a research ethics board was not required.
Results
We present simulated epidemics that assume different amounts of mixing between vaccinated and unvaccinated groups in Figure 1. With 20% baseline immunity among unvaccinated people and 80% of the population vaccinated, we found that the absolute number of cases from vaccinated and unvaccinated groups was similar when mixing was random; however, after we adjusted for the substantially larger population in the vaccinated group, the risk of infection was markedly higher among unvaccinated people during the epidemic. With increased like-with-like mixing, differences in incidence between the vaccinated and unvaccinated groups became more apparent, with cases in the unvaccinated subpopulation accounting for a substantial proportion of infections during the epidemic wave. Like-with-like mixing uncoupled the dynamics of vaccinated and unvaccinated subpopulations, with unvaccinated subpopulations having higher and earlier peak incidence than vaccinated subpopulations. For example, with random mixing, peak incidence was simultaneous in the vaccinated and unvaccinated groups, but with strong like-with-like mixing the epidemic peak among vaccinated people occurred about 1 week later than among unvaccinated people; population-adjusted peak incidence was 4 times higher in the unvaccinated population than in the vaccinated population with random mixing, but about 30 times higher with strong like-with-like mixing (Figure 1).
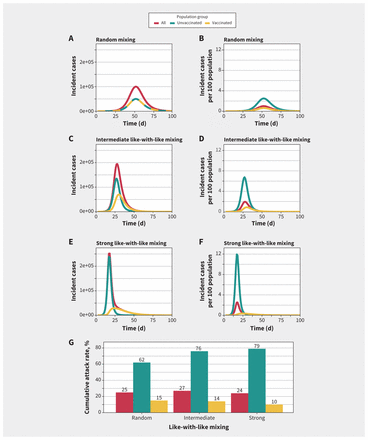
Simulated epidemics for different levels of mixing between vaccinated and unvaccinated populations. (A, C, E) Incident cases and (B, D, F) population-adjusted incidence per 100 population in unvaccinated, vaccinated and overall modelled populations. The degree of like-with-like mixing (assortativity, η) varies from (A, B) random mixing (η = 0) to (C, D) intermediate like-with-like mixing (η = 0.5) to (E, F) near exclusive mixing with people of the same vaccination status (η = 0.9). As like-with-like mixing increases, epidemic size among the vaccinated subpopulation is smaller in absolute terms than among the unvaccinated subpopulation and also has a different contour. (G) Increasing like-with-like mixing increased cumulative attack rates among unvaccinated people and decreased cumulative attack rates among vaccinated people. The highest overall attack rates were seen with intermediate levels of like-with-like mixing.
We found that cumulative attack rates among vaccinated people were highest (15%) with random mixing and lowest (10%) with highly assortative mixing. In contrast, cumulative attack rates were lowest (62%) among unvaccinated people with random mixing, and highest (79%) with highly assortative mixing. The highest cumulative attack rates in the population overall were seen with intermediate levels of like-with-like mixing (27%) compared with random mixing (25%) and strong like-with-like mixing (24%) (Figure 1).
When we varied the degree of like-with-like mixing, changes in epidemic size in the vaccinated subpopulation occurred. As like-with-like mixing increased (i.e., with reduced contact between vaccinated and unvaccinated subpopulations), the final attack rate decreased among vaccinated people, but the contribution of risk to vaccinated people caused by infection acquired from contact with unvaccinated people (as measured by ψ) increased. The larger the value of ψ, the more unvaccinated people contributed to infections in the vaccinated subpopulation.
This pattern was consistent across a range of values for vaccine effectiveness and reproduction numbers (Figure 2). We found that increased like-with-like mixing reduced final outbreak size among vaccinated people most markedly at lower reproduction numbers but increased the value of ψ. With lower vaccine effectiveness, as observed with the Omicron variant, the effects of like-with-like mixing were attenuated. With either lower reproduction numbers or higher vaccine efficacy, transmission was more readily disrupted within the vaccinated subpopulation, such that risk arose increasingly from interactions with the unvaccinated subpopulation, where transmission continued. As like-with-like mixing increased, contribution to infection risk among vaccinated people was increasingly derived from (less and less common) interactions with unvaccinated people, increasing the value of ψ. We found similar patterns in sensitivity analyses in which vaccine coverage was increased from 80% to 99% (Figure 3). Increasing population vaccination coverage decreased the attack rate among vaccinated people (as expected, owing to indirect protective effects) but further increased the relative contribution to risk in vaccinated people by those who were unvaccinated at any level of like-with-like mixing.

Impact of mixing between vaccinated and unvaccinated subpopulations on contribution to risk and final epidemic size for (A) varying reproduction numbers and (B) vaccine effectiveness. Both panels show the impact of increasing like-with-like mixing on outbreak size among the vaccinated subpopulation and contact-adjusted contribution to risk of infection in vaccinated people by unvaccinated people (ψ). As like-with-like mixing (η) increases, the attack rate among vaccinated people decreases, but ψ increases. This relation is seen across a range of (A) initial reproduction numbers and (B) vaccine effectiveness. These effects are more pronounced at lower reproduction numbers and are attenuated as vaccines become less effective. We used a base case estimate of 6 for the reproduction number in the sensitivity analysis on vaccine effectiveness and a base case estimate for vaccine effectiveness of 0.8 in the sensitivity analysis for R.
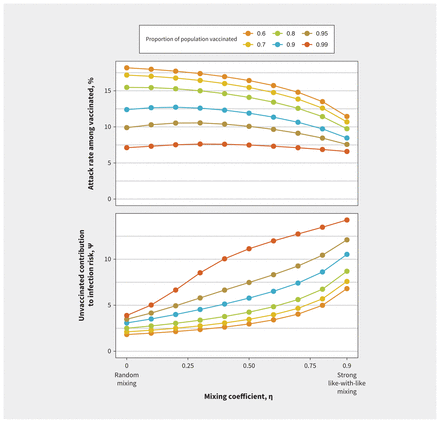
Impact of mixing between vaccinated and unvaccinated subpopulations on contribution to risk and final epidemic size with increasing population vaccination coverage. Increasing population vaccination coverage decreases the attack rate among vaccinated individuals and further increases the relative contribution to risk in vaccinated individuals by the unvaccinated at any level of like-with-like mixing. For levels of vaccination coverage that were evaluated, increasing like-with-like mixing decreases the attack rate among the vaccinated but increases the relative contribution to risk in vaccinated individuals by the unvaccinated.

Comments
Post a Comment